Dell EMC Data Science and BigData Certification Questions and Answers

Question :

If you want to understanding your data at a glance, seeing how data is skewed towards one end, which is the best fit graph or chart.

1. Scatter graph
2. Tree Map
3. Access Mostly Uused Products by 50000+ Subscribers
4. Box-and-whisker plot
Ans : 4
Exp : : Box-and-whisker Plot
Box-and-whisker plots, or boxplots, are an important way to show distributions of data. The name refers to the two parts of the plot: the box, which contains the median of the data along with the 1st and 3rd quartiles
(25% greater and less than the median), and the whiskers, which typically represents data within 1.5 times the Inter-quartile Range (the difference between the 1st and 3rd quartiles). The whiskers can also be used to
also show the maximum and minimum points within the data. When to use box-and-whisker plots: o Showing the distribution of a set of a data: Examples: understanding your data at a glance, seeing how data is skewed
towards one end, identifying outliers in your data.

Question :

Map the followings

1. Clustering
2. Classification
3. Access Mostly Uused Products by 50000+ Subscribers

A. Build models to classify data into different categories
B. Build models to predict continuous data.
C. Find natural groupings and patterns in data.

1. 1-A,2-B,3-C
2. 1-B,2-C,3-A
3. Access Mostly Uused Products by 50000+ Subscribers
4. 1-B,2-A,3-C
Ans : 3
Exp : Classification
Build models to classify data into different categories.
Algorithms: support vector machine (SVM), boosted and bagged decision trees, k-nearest neighbor, Naive Bayes, discriminant analysis, neural networks,

Regression
Build models to predict continuous data.
Algorithms: linear model, nonlinear model, regularization, stepwise regression, boosted and bagged decision trees, neural networks, adaptive neuro-fuzzy learning

Clustering
Find natural groupings and patterns in data.
Algorithms: k-means, hierarchical clustering, Gaussian mixture models, hidden Markov models, self-organizing maps, fuzzy c-means clustering, subtractive clustering,

Question :

Which of the following is not a correct application for the Classification?

1. credit scoring
2. tumor detection
3. Access Mostly Uused Products by 50000+ Subscribers
4. drug discovery
Ans : 4
Exp : Classification : Build models to classify data into different categories
credit scoring, tumor detection, image recognition
Regression: Build models to predict continuous data.
electricity load forecasting, algorithmic trading, drug discovery

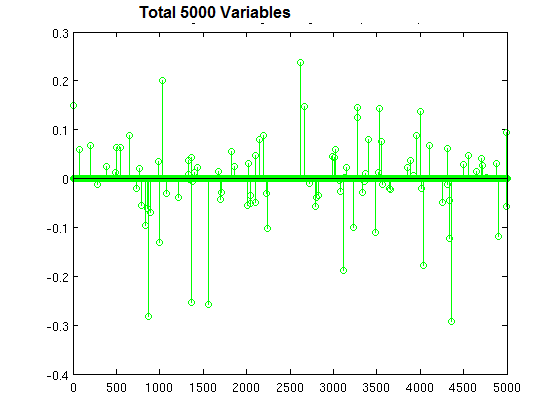
Question : You are building a classifier off of a very high-dimensional data set
similar to shown in the image with 5000 variables (lots of columns, not that many rows).
It can handle both dense and sparse input. Which technique is most suitable, and why?

1. Logistic regression with L1 regularization, to prevent overfitting
2. Naive Bayes, because Bayesian methods act as regularlizers
3. Access Mostly Uused Products by 50000+ Subscribers
4. Random forest, because it is an ensemble method
Ans : 1 Exp : Logistic regression is widely used in machine learning for classification problems. It is well-known that regularization is required to avoid over-fitting, especially when there is a only small number
of training examples, or when there are a large number of parameters to be learned. In particular, L1 regularized logistic regression is often used for feature selection, and has been shown to have good generalization
performance in the presence of many irrelevant features. (Ng 2004; Goodman 2004) Unregularized logistic regression is an unconstrained con-vex optimization problem with a continuously differentiable objective
function. As a consequence, it can be solved fairly efficiently with standard convex optimization methods, such as Newton's method or conjugate gradient. However, adding the L1 regularization makes the optimization
problem com-putationally more expensive to solve. If the L1 regulariza-tion is enforced by an L1 norm constraint on the parameLogistic regression is a classifier, and L1 regularization tends to produce models that
ignore dimensions of the input that are not predictive. This is particularly useful when the input contains many dimensions. k-nearest neighbors classification is also a classification technique, but relies on notions
of distance. In a high-dimensional space, most every data point is "far" from others (the curse of dimensionality) and so these techniques break down. Naive Bayes is not inherently regularizing. Random forests
represent an ensemble method, but an ensemble method is not necessarily more suitable to high-dimensional data. Practically, I think the biggest reasons for regularization are 1) to avoid overfitting by not generating
high coefficients for predictors that are sparse. 2) to stabilize the estimates especially when there's collinearity in the data.
1) is inherent in the regularization framework. Since there are two forces pulling each other in the objective function, if there's no meaningful loss reduction, the increased penalty from the regularization term
wouldn't improve the overall objective function. This is a great property since a lot of noise would be automatically filtered out from the model.
To give you an example for 2), if you have two predictors that have same values, if you just run a regression algorithm on it since the data matrix is singular, your beta coefficients will be Inf if you try to do a
straight matrix inversion. But if you add a very small regularization lambda to it, you will get stable beta coefficients with the coefficient values evenly divided between the equivalent two variables.
For the difference between L1 and L2, the following graph demonstrates why people bother to have L1 since L2 has such an elegant analytical solution and is so computationally straightforward. Regularized regression
can also be represented as a constrained regression problem (since they are Lagrangian equivalent). The implication of this is that the L1 regularization gives you sparse estimates. Namely, in a high dimensional
space, you got mostly zeros and a small number of non-zero coefficients. This is huge since it incorporates variable selection to the modeling problem. In addition, if you have to score a large sample with your model,
you can have a lot of computational savings since you don't have to compute features(predictors) whose coefficient is 0. I personally think L1 regularization is one of the most beautiful things in machine learning and
convex optimization. It is indeed widely used in bioinformatics and large scale machine learning for companies like Facebook, Yahoo, Google and Microsoft.

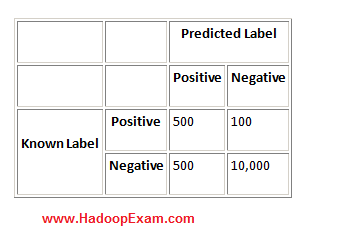
Question : Consider the following confusion matrix for a data set with out of , instances positive:

In this case, Precision = 50%, Recall = 83%, Specificity = 95%, and Accuracy = 95%.
Select the correct statement

1. Precision is low, which means the classifier is predicting positives best
2. Precision is low, which means the classifier is predicting positives poorly
3. Access Mostly Uused Products by 50000+ Subscribers
4. 1 and 3
5. 2 and 3
Ans : 5
Exp : In this case, Precision = 50%, Recall = 83%, Specificity = 95%, and Accuracy = 95%. In this case, Precision is low, which means the classifier is predicting positives poorly. However, the three other measures
seem to suggest that this is a good classifier. This just goes to show that the problem domain has a major impact on the measures that should be used to evaluate a classifier within it, and that looking at the 4
simple cases presented is not sufficient.

Question : From the , sample books you have based on the title, prepface, author, publisher you want to classify and used trained a binary classifier
and after running against your test set (13000 Sample books data) . It correctly classified 5000 books as belonging to Software Books and 4000 books
are not software books. And also incorrectly classified 1000 books as belonging to software books and 3000 books not belonging to software book.
What is the recall for your trained classifier on this test dataset?

1. 0.500
2. 0.600
3. Access Mostly Uused Products by 50000+ Subscribers
4. 0.750
5. 1.00
Ans : 3 Exp : In pattern recognition and information retrieval with binary classification, precision (also called positive predictive value) is the fraction of retrieved instances that are relevant, while recall (also
known as sensitivity) is the fraction of relevant instances that are retrieved. Both precision and recall are therefore based on an understanding and measure of relevance. Suppose a program for recognizing dogs in
scenes from a video identifies 7 dogs in a scene containing 9 dogs and some cats. If 4 of the identifications are correct, but 3 are actually cats, the program's precision is 4/7 while its recall is 4/9. When a search
engine returns 30 pages only 20 of which were relevant while failing to return 40 additional relevant pages, its precision is 20/30 = 2/3 while its recall is 20/60 = 1/3. In statistics, if the null hypothesis is that
all and only the relevant items are retrieved, absence of type I and type II errors corresponds respectively to maximum precision (no false positive) and maximum recall (no false negative). The above pattern
recognition example contained 7 - 4 = 3 type I errors and 9 - 4 = 5 type II errors. Precision can be seen as a measure of exactness or quality, whereas recall is a measure of completeness or quantity. In simple terms,
high precision means that an algorithm returned substantially more relevant results than irrelevant, while high recall means that an algorithm returned most of the relevant results. 5000 books were software books, and
correctly identified as such (true positives). 3000 other books were software books but not identified as such (false negatives). Recall = TP / (TP+FN) = 5000 / (5000 + 3000) = 0.625
sensitivity or true positive rate (TPR)
eqv. with hit rate, recall
{TPR} = {TP} / P = {TP} / ({TP}+{FN})
specificity (SPC) or True Negative Rate
{SPC} = {TN} / N = {TN} / ({FP} + {TN})
precision or positive predictive value (PPV)
{PPV} = {TP} / ({TP} + {FP})
negative predictive value (NPV)
{NPV} = {TN} / ({TN} + {FN})
fall-out or false positive rate (FPR)
{FPR} = {FP} / N = {FP} / ({FP} + {TN})
false discovery rate (FDR)
{FDR} = {FP} / ({FP} + {TP}) = 1 - {PPV}
false negative rate (FNR)
{FNR} = {FN} / ({FN} + {TP}) = 1 - {TPR}

Question : Let's say we want to insert the strings "foo" and "bar" into a Bloom filter that is bits wide, and we have two hash functions.
1. Compute the two hashes of "foo", and get the values 1 and 6.
2. Set bits 1 and 6 in the bit array.
3. Access Mostly Uused Products by 50000+ Subscribers
4. Set bits 6 and 3 in the bit array.

Suppose we now want to query the Bloom filter, to see whether the value "baz" are present.
Compute the two hashes of "baz", and get the values 1 and 3

So after that we will report

1. true positive
2. false positive
3. Access Mostly Uused Products by 50000+ Subscribers
4. false negative
Ans : 2
Exp : Suppose we now want to query the Bloom filter, to see whether the values "quux" and "baz" are present.
1. Compute the two hashes of "quux", and get the values 4 and 0.
2. Check bit 4 in the bit array. It is not set, so "quux" cannot be present. We do not need to check bit 0.
3. Access Mostly Uused Products by 50000+ Subscribers
4. Check bit 1 in the bit array. It is set, as is bit 3, so we say that "baz" is present even though it is not. We have reported a false positive.

Question : Select the correct statement which applies to K-Mean Clustering?

1. When the numbers of data are not so many, initial grouping will determine the cluster significantly.
2. The number of cluster, K, must be determined before hand.
3. Access Mostly Uused Products by 50000+ Subscribers
4. We never know which attribute contributes more to the grouping process since we assume that each attribute has the same weight.

1. 1,2
2. 2,3
3. Access Mostly Uused Products by 50000+ Subscribers
4. 2,3,4
5. All 1,2,3 and 4

Ans : 5
Exp : What are the weaknesses of K-Mean Clustering?
Similar to other algorithm, K-mean clustering has many weaknesses:
- When the numbers of data are not so many, initial grouping will determine the cluster significantly.
- The number of cluster, K, must be determined beforehand.
- We never know the real cluster, using the same data, if it is inputted in a different way may produce different cluster if the number of data is a few.
- We never know which attribute contributes more to the grouping process since we assume that each attribute has the same weight.
One way to overcome those weaknesses is to use K-mean clustering only if there are available many data.

Question : Suppose you have several objects and each object have several attributes and you want
to classify the objects based on the attributes, then you can apply K-Mean Clustering?

1. True
2. False

Ans : 1
Exp :

There are a lot of applications of the K-mean clustering, range from unsupervised learning of neural network,
Pattern recognitions, Classification analysis, Artificial intelligent, image processing, machine vision, etc. In principle, you have several objects and each object have several attributes and you want to classify the
objects based on the attributes, then you can apply this algorithm.

Question : KMeans is a clustering algorithm. Its purpose is to partition a set of vectors into K groups
that cluster around common mean vector. This can also be thought as approximating the input each of the input
vector with one of the means, so the clustering process finds, in principle, the best dictionary or codebook to
vector quantize the data.What is the best way to ensure that this algorithm will find a good clustering of a input
collection of vectors?

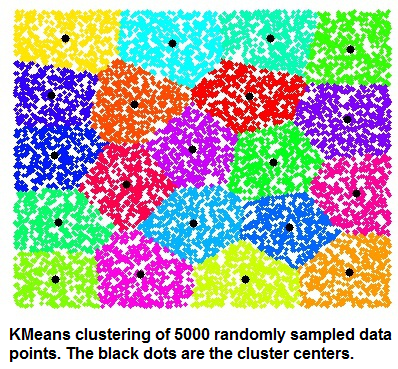
1. Choose the initial centroids so that they are having average distance among all the distances.
2. Run at least log(N) iterations of Lloyd's algorithm, where N is the number of observations in the data set
3. Access Mostly Uused Products by 50000+ Subscribers
4. Choose the initial centroids so that they are far away from each other

Ans : 4
Exp : The k-means algorithm takes as input the number of clusters to generate, k, and a set of observation vectors to cluster. It returns a set of centroids, one for each of the k clusters. An observation vector is
classified with the cluster number or centroid index of the centroid closest to it.

A vector v belongs to cluster i if it is closer to centroid i than any other centroids. If v belongs to i, we say centroid i is the dominating centroid of v. The k-means algorithm tries to minimize distortion, which
is defined as the sum of the squared distances between each observation vector and its dominating centroid. Each step of the k-means algorithm refines the choices of centroids to reduce distortion. The change in
distortion is used as a stopping criterion: when the change is lower than a threshold, the k-means algorithm is not making sufficient progress and terminates. One can also define a maximum number of iterations.

Since vector quantization is a natural application for k-means, information theory terminology is often used. The centroid index or cluster index is also referred to as a "code" and the table mapping codes to
centroids and vice versa is often referred as a "code book". The result of k-means, a set of centroids, can be used to quantize vectors. Quantization aims to find an encoding of vectors that reduces the expected
distortion. This question is about the properties that make k-means an effective clustering heuristic, which primarily deal with ensuring that the initial centers are far away from each other. This is how modern
k-means algorithms like k-means++ guarantee that with high probability Lloyd's algorithm will find a clustering within a constant factor of the optimal possible clustering for each k.
All routines expect obs to be a M by N array where the rows are the observation vectors. The codebook is a k by N array where the i'th row is the centroid of code word i. The observation vectors and centroids have the
same feature dimension. As an example, suppose we wish to compress a 24-bit color image (each pixel is represented by one byte for red, one for blue, and one for green) before sending it over the web. By using a
smaller 8-bit encoding, we can reduce the amount of data by two thirds. Ideally, the colors for each of the 256 possible 8-bit encoding values should be chosen to minimize distortion of the color. Running k-means with
k=256 generates a code book of 256 codes, which fills up all possible 8-bit sequences. Instead of sending a 3-byte value for each pixel, the 8-bit centroid index (or code word) of the dominating centroid is
transmitted. The code book is also sent over the wire so each 8-bit code can be translated back to a 24-bit pixel value representation. If the image of interest was of an ocean, we would expect many 24-bit blues to be
represented by 8-bit codes. If it was an image of a human face, more flesh tone colors would be represented in the code book.k-means clustering is a method of vector quantization, originally from signal processing,
that is popular for cluster analysis in data mining. k-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype
of the cluster. This results in a partitioning of the data space into Voronoi cells. The problem is computationally difficult (NP-hard); however, there are efficient heuristic algorithms that are commonly employed and
converge quickly to a local optimum. These are usually similar to the expectation-maximization algorithm for mixtures of Gaussian distributions via an iterative refinement approach employed by both algorithms.
Additionally, they both use cluster centers to model the data; however, k-means clustering tends to find clusters of comparable spatial extent, while the expectation-maximization mechanism allows clusters to have
different shapes

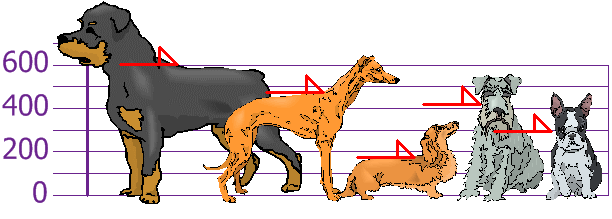
Question : You and your friends have just measured the heights of your dogs (in millimetres):
The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.
Find out the Variance

1. 2000
2. 20000
3. Access Mostly Uused Products by 50000+ Subscribers
4. Not enough information to calculate the mean

Correct Answer : Get Lastest Questions and Answer : To calculate the Variance, take each difference, square it, and then average the result

Explanation: Variance = (square(206) + square(76) + square(-224) + square(36) + square(-94))/5
= 108,520/5 = 21,704

Question : You and your friends have just measured the heights of your dogs (in millimetres):
The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.
Find out the Standard Deviation

1. 147
2. 140
3. Access Mostly Uused Products by 50000+ Subscribers
4. Not enough information to calculate the mean

Correct Answer : Get Lastest Questions and Answer : To calculate the Variance, take each difference, square it, and then average the result

Explanation: Variance = (square(206) + square(76) + square(-224) + square(36) + square(-94))/5
= 108,520/5 = 21,704
And the Standard Deviation is just the square root of Variance, so: square root of 21,704 = 147.32 = 147

Question : All HadoopExam website subscribers information is stored in the MySQL database,
Which tool is best suited to import a portion of a subscribers information every day as files into HDFS,
and generate Java classes to interact with that imported data?

1. Hive
2. Pig
3. Access Mostly Uused Products by 50000+ Subscribers
4. Flume

Correct Answer : Get Lastest Questions and Answer :

Explanation: Sqoop ("SQL-to-Hadoop") is a straightforward command-line tool with the following capabilities:
" Imports individual tables or entire databases to files in HDFS
" Generates Java classes to allow you to interact with your imported data
" Provides the ability to import from SQL databases straight into your Hive data warehouse
After setting up an import job in Sqoop, you can get started working with SQL database-backed data from your Hadoop MapReduce cluster in minutes.

The input to the import process is a database table. Sqoop will read the table row-by-row into HDFS. The output of this import process is a set of files containing a copy of the imported table. The import process is
performed in parallel. For this reason, the output will be in multiple files. These files may be delimited text files (for example, with commas or tabs separating each field), or binary Avro or SequenceFiles
containing serialized record data.

A by-product of the import process is a generated Java class which can encapsulate one row of the imported table. This class is used during the import process by Sqoop itself. The Java source code for this class is
also provided to you, for use in subsequent MapReduce processing of the data. This class can serialize and deserialize data to and from the SequenceFile format. It can also parse the delimited-text form of a record.
These abilities allow you to quickly develop MapReduce applications that use the HDFS-stored records in your processing pipeline. You are also free to parse the delimiteds record data yourself, using any other tools
you prefer.

Watch the module : 22 from http://hadoopexam.com/index.html/#hadoop-training

Dell EMC Data Science and BigData Certification Questions and Answers

Related Questions