Dell EMC Data Science and BigData Certification Questions and Answers

Question : In linear regression modeling, which action can be taken to improve the linearity of the relationship
between the dependent and independent variables?


1. Apply a transformation to a variable
2. Use a different statistical package
3. Access Mostly Uused Products by 50000+ Subscribers
4. Change the units of measurement on the independent variable



Correct Answer : Get Lastest Questions and Answer : Exp: In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variable) denoted X.
The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. (This term should be distinguished from multivariate
linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.)

In linear regression, data are modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, linear regression refers to a
model in which the conditional mean of y given the value of X is an affine function of X. Less commonly, linear regression could refer to a model in which the median, or some other quantile of the conditional
distribution of y given X is expressed as a linear function of X. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of y given X, rather than on the joint
probability distribution of y and X, which is the domain of multivariate analysis.

Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications.[4] This is because models which depend linearly on their unknown parameters
are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.

Linear regression has many practical uses. Most applications fall into one of the following two broad categories:

If the goal is prediction, or forecasting, or reduction, linear regression can be used to fit a predictive model to an observed data set of y and X values. After developing such a model, if an additional value of X is
then given without its accompanying value of y, the fitted model can be used to make a prediction of the value of y.
Given a variable y and a number of variables X1, ..., Xp that may be related to y, linear regression analysis can be applied to quantify the strength of the relationship between y and the Xj, to assess which Xj may
have no relationship with y at all, and to identify which subsets of the Xj contain redundant information about y.
Linear regression models are often fitted using the least squares approach, but they may also be fitted in other ways, such as by minimizing the "lack of fit" in some other norm (as with least absolute deviations
regression), or by minimizing a penalized version of the least squares loss function as in ridge regression (L2-norm penalty) and lasso (L1-norm penalty). Conversely, the least squares approach can be used to fit
models that are not linear models. Thus, although the terms "least squares" and "linear model" are closely linked, they are not synonymous.






Question : Data visualization is used in the final presentation of an analytics project. For what else is this
technique commonly used?


1. ETLT
2. Descriptive statistics
3. Access Mostly Uused Products by 50000+ Subscribers
4. Model selection



Correct Answer : Get Lastest Questions and Answer :
Exp: The adoption of Big Data tools and technology heavily relies on distributed scaled out computing. One of the main differences in this setting is that it includes systems that operate as a whole on top of several
independent hosts. These hosts coordinate their actions with limited information and as a result maintenance complexity significantly increases. One way to overcome this challenge is smart data visualization, which
helps the IT experts and management pinpoint the source of problems quickly.

The need for smart visualization is not unique to this problem. Representing complex data as a concise picture which tells decision-makers a story is a key part of any data analytics or data science project. Valuable
results of a rigorous analysis may remain undiscovered due to a lack of a visualization clearly communicating the underlying information to the reader. The importance of data visualization is not a novelty. A number
of visualization tools, as well as a general interest in data visualization topics, have exploded in popularity in recent years, as evidenced by the proliferation of literature available about infographics and
visualization arcanum in both print and online media.


Executive customers of the Data Science-as-a-Service (DSaaS) team can't review every detail in the data they use. In order to make data-driven decisions and draw conclusions, what they need is a distilled version of
the data. This is where smart visualization can be of the highest importance. It can allow readers understand "what is going on" in the data in just a few moments instead of having to undertake an annoying, time
consuming analysis.

Nowadays, advanced data visualizations go beyond graphs and charts to help in the process of making crucial business decisions. Several visualization formats are available: static, zooming, clickable, animated, video,
or interactive. The choice between these depends on the overall objectives of the visualization. While static is the simplest and the most common form of visualization, the interactive options are becoming more
popular because they give users some control over the displayed information






Question : You have been assigned to do a study of the daily revenue effect of a pricing model of online
transactions. All the data currently available to you has been loaded into your analytics database;
revenue data, pricing data, and online transaction data. You find that all the data comes in
different levels of granularity. The transaction data has timestamps (day, hour, minutes, seconds),
pricing is stored at the daily level, and revenue data is only reported monthly. What is your next
step?



1. Interpolate a daily model for revenue from the monthly revenue data.
2. Aggregate all data to the monthly level in order to create a monthly revenue model.
3. Access Mostly Uused Products by 50000+ Subscribers
question.
4. Disregard revenue as a driver in the pricing model, and create a daily model based on pricing
and transactions only.



Correct Answer : Get Lastest Questions and Answer :
Exp:

Related Questions

---

Question : You have been assigned to run a logistic regression model for each of countries, and all the
data is currently stored in a PostgreSQL database. Which tool/library would you use to produce
these models with the least effort?

1. RStudio
2. MADlib
3. Access Mostly Uused Products by 50000+ Subscribers
4. HBase


Question : Imagine you are trying to hire a Data Scientist for your team. In addition to technical ability and
quantitative background, which additional essential trait would you look for in people applying for
this position?



1. Communication skill
2. Scientific background
3. Access Mostly Uused Products by 50000+ Subscribers
4. Well Organized




Question : What describes the use of UNION clause in a SQL statement?

1. Operates on queries and potentially decreases the number of rows
2. Operates on queries and potentially increases the number of rows
3. Access Mostly Uused Products by 50000+ Subscribers
4. Operates on both tables and queries and potentially increases both the number of rows and columns




Question : You have run the association rules algorithm on your data set, and the two rules {banana, apple}
=> {grape} and {apple, orange}=> {grape} have been found to be relevant. What else must be true?



1. {grape, apple, orange} must be a frequent itemset.
2. {banana, apple, grape, orange} must be a frequent itemset.
3. Access Mostly Uused Products by 50000+ Subscribers
4. {banana, apple} => {orange} must be a relevant rule.


similar interests. For example, association rules may suggest that those customers who have bought product A have also bought product B, or those customers who have bought products A, B, and C are more similar to this
customer. These findings provide opportunities for retailers to cross-sell their products. Association rule mining is primarily focused on finding frequent co-occurring associations among a collection of items. It is
sometimes referred to as "Market Basket Analysis", since that was the original application area of association mining. The goal is to find associations of items that occur together more often than you would expect
from a random sampling of all possibilities. The classic example of this is the famous Beer and Diapers association that is often mentioned in data mining books. The story goes like this: men who go to the store to
buy diapers will also tend to buy beer at the same time. Let us illustrate this with a simple example. Suppose that a store's retail transactions database includes the following information:

There are 600,000 transactions in total.
7,500 transactions contain diapers (1.25 percent)
60,000 transactions contain beer (10 percent)
6,000 transactions contain both diapers and beer (1.0 percent)
If there was no association between beer and diapers (i.e., they are statistically independent), then we expect only 10% of diaper purchasers to also buy beer (since 10% of all customers buy beer). However, we
discover that 80% (=6000/7500) of diaper purchasers also buy beer. This is a factor of 8 increase over what was expected - that is called Lift, which is the ratio of the observed frequency of co-occurrence to the
expected frequency. This was determined simply by counting the transactions in the database. So, in this case, the association rule would state that diaper purchasers will also buy beer with a Lift factor of 8. In
statistics, Lift is simply estimated by the ratio of the joint probability of two items x and y, divided by the product of their individual probabilities: Lift = P(x,y)/[P(x)P(y)]. If the two items are statistically
independent, then P(x,y)=P(x)P(y), corresponding to Lift = 1 in that case. Note that anti-correlation yields Lift values less than 1, which is also an interesting discovery - corresponding to mutually exclusive items
that rarely co-occur together.



Question : When would you use a Wilcoxson Rank Sum test?

1. When the data can easily be sorted
2. When the populations represent the sums of other values
3. Access Mostly Uused Products by 50000+ Subscribers
4. When you cannot make an assumption about the distribution of the populations


Question : In the MapReduce framework, what is the purpose of the Reduce function?


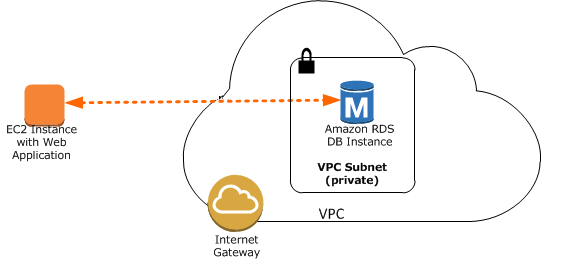
1. It writes the output of the Map function to storage
2. It breaks the input into smaller components and distributes to other nodes in the cluster
3. Access Mostly Uused Products by 50000+ Subscribers
4. It distributes the input to multiple nodes for processing



Question : Which of the following is an example of quasi-structured data?

1. OLAP
2. Customer record table
3. Access Mostly Uused Products by 50000+ Subscribers
4. OLTP