Cloudera Databricks Data Science Certification Questions and Answers (Dumps and Practice Questions)

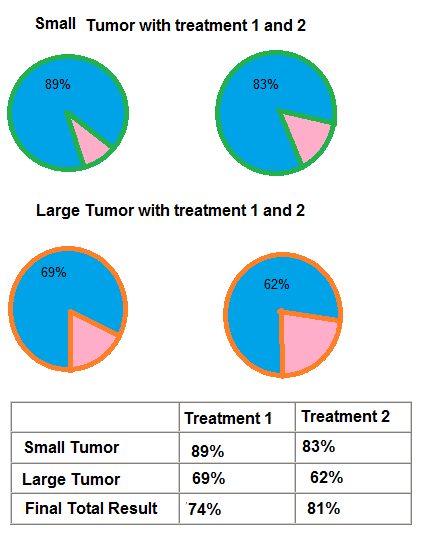
Question :Consider the given table in the image of success rates for two
different treatments of Brain Tumor Cancer for two classes of patients with small tumor and large tumor.
When we look at the treatments overall, treatment 2 has a higher success rate,
but when we look at the treatments for individual patient types,
treatment 1 has a higher success rate. Select the correct statement from below?

1. few patients had large tumor and treatment 2
2. few patients had small tumor and treatment 1
3. Access Mostly Uused Products by 50000+ Subscribers

Correct Answer : Get Lastest Questions and Answer : Exp: What Is Simpson's Paradox?
With all data, we need to exercise caution. Where did it come from? How was it obtained? And what is it really saying? These are all good questions that we should ask when presented with data. Sometimes what the data seem to be saying is not really the case. Consider the very surprising case of Simpson's paradox.
A paradox is something that on the surface seems contradictory. Paradoxes help to reveal underlying truth beneath the surface of what appears to be absurd. In particular Simpson's paradox demonstrates what kinds of problems result from combining data from several groups. An Overview of the Paradox. Suppose we are observing several groups, and establish a relationship or correlation for each of these groups. Simpson's paradox says that when we combine all of the groups together, and look at the data in aggregate form, the correlation that we noticed before may reverse itself. This is most often due to lurking variables that have not been considered, but sometimes it is due to the numerical values of the data. Simpson's Paradox occurs when a trend present in independent datasets reverses when the datasets are combined. Simpson's Paradox disappears when causal information is considered. In this case, we can assume that large kidney stones are harder to treat successfully than small kidney stones. If treatment 1 is used more often on patients with large tumor than treatment 2 is, then even though treatment 2 is more successful than treatment 1, treatment 1 may have an overall lower success rate than treatment 2. Every Simpson's paradox involves at least three variables:
the explained,the observed explanatory, the lurking explanatory : If the effect of the observed explanatory variable on the explained variable changes directions when you account for the lurking explanatory variable, you've got a Simpson's Paradox. For example, to the right, x appears to have a negative effect on y, but the opposite is true when you account for color. y is the explained variable, x the observed explanatory variable, and color the lurking explanatory variable.What Simpson's paradox is not
Simpson's: It was first mentioned by British statistician Udny Yule in 1903.
A paradox: Simpson's paradox is just a special case of ommitted variable bias. W.V. Quine would call it a veridical paradox.
Every ommitted variable problem: Women earn only 77 percent of what men do, but according to Cornell economists Francine Blau and Lawrence Kahn, accounting for work experience, education, industry, and unionization shrinks the gap to 91 percent (p. 52). So, discrimination matters less than the `77 percent` stat would lead you to believe. But is this Simpson's paradox? No, because the correction isn't large enough for the effect of gender to change sign.
Why it matters: Simpson's paradox usually fools us on tests of performance. In a famous example, researchers concluded that a newer treatment for kidney stones was more effective than traditional surgery, but it was later revealed that the newer treatment was more often being used on small kidney stones. More recently, on elementary school tests, minority students in Texas outperform their peers in Wisconsin, but Texas has so many minority students that Wisconsin beats it in state rankings. It would be a shame if Simpson's paradox led doctors to prescribe ineffective treatments or Texas schools to waste money copying Wisconsin.

Question : Consider the given table in the image of success rates for two
different treatments of Brain Tumor Cancer for two classes of patients with small tumor and large tumor.
In case of a large tumor what would we suggest for treatment, treatment 1 or treatment 2.
If we know that a particular patient has large brain tumor, are we better off recommending treatment 1 or treatment 1?

1. Treatment 1, because it has been proven better for patients who are known to have large stones
2. It depends on whether or not we believe the size of the tumor influences the choice of each treatment
3. Access Mostly Uused Products by 50000+ Subscribers
4. We should consider other information about the patient, such as their age and gender, before we make a decision

Correct Answer : Get Lastest Questions and Answer :
Explanation: What Is Simpson's Paradox?
With all data, we need to exercise caution. Where did it come from? How was it obtained? And what is it really saying? These are all good questions that we should ask when presented with data. Sometimes what the data seem to be saying is not really the case. Consider the very surprising case of Simpson's paradox.
A paradox is something that on the surface seems contradictory. Paradoxes help to reveal underlying truth beneath the surface of what appears to be absurd. In particular Simpson's paradox demonstrates what kinds of problems result from combining data from several groups.
An Overview of the Paradox. Suppose we are observing several groups, and establish a relationship or correlation for each of these groups. Simpson's paradox says that when we combine all of the groups together, and look at the data in aggregate form, the correlation that we noticed before may reverse itself. This is most often due to lurking variables that have not been considered, but sometimes it is due to the numerical values of the data.
By Simpson's paradox, the fact that treatment 2 is overall more effective could be a misleading result, as treatment 2 performs better in the data sample with both classes of tumor. This could occur if there is a confounding variable: for example, perhaps large tumor are harder to treat and so the more effective treatment 1 is more often applied to these harder cases. This data sample does not prove, however, that treatment 1 is better for large tumor. It is also possible that there is no such confounding variable in which case the correct conclusion would that 2 is overall more effective. Every Simpson's paradox involves at least three variables:
the explained,the observed explanatory, the lurking explanatory : If the effect of the observed explanatory variable on the explained variable changes directions when you account for the lurking explanatory variable, you've got a Simpson's Paradox. For example, to the right, x appears to have a negative effect on y, but the opposite is true when you account for color. y is the explained variable, x the observed explanatory variable, and color the lurking explanatory variable.What Simpson's paradox is not
Simpson's: It was first mentioned by British statistician Udny Yule in 1903.
A paradox: Simpson's paradox is just a special case of ommitted variable bias. W.V. Quine would call it a veridical paradox.
Every ommitted variable problem: Women earn only 77 percent of what men do, but according to Cornell economists Francine Blau and Lawrence Kahn, accounting for work experience, education, industry, and unionization shrinks the gap to 91 percent (p. 52). So, discrimination matters less than the `77 percent` stat would lead you to believe. But is this Simpson's paradox? No, because the correction isn't large enough for the effect of gender to change sign.
Why it matters: Simpson's paradox usually fools us on tests of performance. In a famous example, researchers concluded that a newer treatment for kidney stones was more effective than traditional surgery, but it was later revealed that the newer treatment was more often being used on small kidney stones. More recently, on elementary school tests, minority students in Texas outperform their peers in Wisconsin, but Texas has so many minority students that Wisconsin beats it in state rankings. It would be a shame if Simpson's paradox led doctors to prescribe ineffective treatments or Texas schools to waste money copying Wisconsin.

Question : Consider the given table in the image of success rates for two
different treatments of Brain Tumor Cancer for two classes of patients with small tumor and large tumor.
We get to know that for large timor patients treatment 1 will be used. So in case of small tumor which treatment
should be recommended.

1. Treatment 1, which has proved that small tumor has 89% success ratio.
2. We have to find that the size of the tumor realy metter or not.
3. Access Mostly Uused Products by 50000+ Subscribers
4. As we see totally treatment 2 has been proved better.

Correct Answer : Get Lastest Questions and Answer :
Explanation: What Is Simpson's Paradox?
With all data, we need to exercise caution. Where did it come from? How was it obtained? And what is it really saying? These are all good questions that we should ask when presented with data. Sometimes what the data seem to be saying is not really the case. Consider the very surprising case of Simpson's paradox.
A paradox is something that on the surface seems contradictory. Paradoxes help to reveal underlying truth beneath the surface of what appears to be absurd. In particular Simpson's paradox demonstrates what kinds of problems result from combining data from several groups.
An Overview of the Paradox Suppose we are observing several groups, and establish a relationship or correlation for each of these groups. Simpson's paradox says that when we combine all of the groups together, and look at the data in aggregate form, the correlation that we noticed before may reverse itself. This is most often due to lurking variables that have not been considered, but sometimes it is due to the numerical values of the data.
By Simpson's paradox, the fact that treatment 2 is overall more effective could be a misleading result, as treatment 1 performs better in the data sample with both classes of tumor. This could occur if there is a confounding variable: for example, perhaps large tumors are harder to treat and so the more effective treatment 1 is more often applied to these harder cases. We are given that there is in fact a confounding variable. So we can conclude that the data indicates that treatment 1 performs better or small (and large) tumor. Every Simpson's paradox involves at least three variables:
the explained,the observed explanatory, the lurking explanatory : If the effect of the observed explanatory variable on the explained variable changes directions when you account for the lurking explanatory variable, you've got a Simpson's Paradox. For example, to the right, x appears to have a negative effect on y, but the opposite is true when you account for color. y is the explained variable, x the observed explanatory variable, and color the lurking explanatory variable.What Simpson's paradox is not
Simpson's: It was first mentioned by British statistician Udny Yule in 1903.
A paradox: Simpson's paradox is just a special case of ommitted variable bias. W.V. Quine would call it a veridical paradox.
Every ommitted variable problem: Women earn only 77 percent of what men do, but according to Cornell economists Francine Blau and Lawrence Kahn, accounting for work experience, education, industry, and unionization shrinks the gap to 91 percent (p. 52). So, discrimination matters less than the `77 percent` stat would lead you to believe. But is this Simpson's paradox? No, because the correction isn't large enough for the effect of gender to change sign.
Why it matters: Simpson's paradox usually fools us on tests of performance. In a famous example, researchers concluded that a newer treatment for kidney stones was more effective than traditional surgery, but it was later revealed that the newer treatment was more often being used on small kidney stones. More recently, on elementary school tests, minority students in Texas outperform their peers in Wisconsin, but Texas has so many minority students that Wisconsin beats it in state rankings. It would be a shame if Simpson's paradox led doctors to prescribe ineffective treatments or Texas schools to waste money copying Wisconsin.

Cloudera Databricks Data Science Certification Questions and Answers (Dumps and Practice Questions)

Related Questions