Cloudera Databricks Data Science Certification Questions and Answers (Dumps and Practice Questions)

Question : In probability theory, a conditional probability measures the probability of an event given that
(by assumption, presumption, assertion or evidence) another event has occurred. So how do you represent P(X,Y,Z)?



1. P(X,Y|Z)P(Y|Z)P(Z)
2. P(X|Y,Z)P(Y|Z)P(Z)
3. Access Mostly Uused Products by 50000+ Subscribers
4. P(X)P(Y)P(Z)
5. P(X)P(Y)P(Z|X,Y)




Correct Answer : Get Lastest Questions and Answer :
Explanation: From the definition, P(X,Y|Z) P(Y|Z) =P(X,Y,Z)/P(Z) P(Y,Z)/P(Z) =P(X,Y,Z) P(Y,Z) =P(X|Y,Z)
This follows from the definition of conditional probability, applied twice: P(X,Y)=(PX|Y)P(Y)
Let's look at some other problems in which we are asked to find a conditional probability.

Example 1: A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a black marble and then a white marble is 0.34, and the probability of selecting a black marble on the first draw is 0.47. What is the probability of selecting a white marble on the second draw, given that the first marble drawn was black?
Solution:
P(White|Black) = P(Black and White)/P(Black) = 0.34/0.47 = 0.72 = 72%

Example 2: The probability that it is Friday and that a student is absent is 0.03. Since there are 5 school days in a week, the probability that it is Friday is 0.2. What is the probability that a student is absent given that today is Friday?
Solution:
P(Absent|Friday) = P(Friday and Absent)/P(Friday) = 0.03/0.2 = 0.15 = 15%

Example 3: At Kennedy Middle School, the probability that a student takes Technology and Spanish is 0.087. The probability that a student takes Technology is 0.68. What is the probability that a student takes Spanish given that the student is taking Technology?
Solution:
P(Spanish|Technology) = P(Technology and Spanish)/P(Technology) = 0.087/0.68 = 0.13 = 13%









Question : The use of log probabilities is widespread in several fields of computer science such
as information theory and natural language processing because


1. Speed. Since multiplication is more expensive than addition, taking the product of a high number of probabilities is faster
if they are represented in log form. (The conversion to log form is expensive, but is only incurred once.)

2. Accuracy. The use of log probabilities improves numerical stability.
3. Access Mostly Uused Products by 50000+ Subscribers
4. Only 1 and 3
5. Only 1,2 and 3



Correct Answer : Get Lastest Questions and Answer :


Explanation: 1.Speed. Since multiplication is more expensive than addition, taking the product of a high number of probabilities is faster if they are represented in log form. (The conversion to log form is expensive, but is only incurred once.)
2.Accuracy. The use of log probabilities improves numerical stability.
The use of log probabilities is widespread in several fields of computer science such as information theory and natural language processing as it represents the surprisal, the minimum length of the message that specifies the outcome in an optimally efficient code.

The log of the product of probabilities is simply the sum of logs of those probabilities, which is easy to compute.
The log of the sum of probabilities does not give rise to any similar shortcut, and so a transformation to log space does not help.

Because probabilities cannot exceed 1.0, getting a very large product of probabilities -- overflow -- is not a problem. But, probabilities can be very small, and their product smaller still, so underflows (very small positive values) are a real problem, especially in contexts like Bayes nets. However, the log of very small values does not have a small absolute value, and so working in log space avoids underflow.

Working in log space does not impact the time to convergence for MLE or gradient descent.








Question : Select the correct statement which applies to calculate the probabilities in log space?

1. It is more efficient to divide probabilities in log space
2. It is more efficient to substract probabilities in log space
3. Access Mostly Uused Products by 50000+ Subscribers
4. It is more efficient to sum probabilities in log space




Correct Answer : Get Lastest Questions and Answer :


Explanation:Speed. Since multiplication is more expensive than addition, taking the product of a high number of probabilities is faster if they are represented in log form. (The conversion to log form is expensive, but is only incurred once.)
2.Accuracy. The use of log probabilities improves numerical stability.
The use of log probabilities is widespread in several fields of computer science such as information theory and natural language processing as it represents the surprisal, the minimum length of the message that specifies the outcome in an optimally efficient code.

The log of the product of probabilities is simply the sum of logs of those probabilities, which is easy to compute.
The log of the sum of probabilities does not give rise to any similar shortcut, and so a transformation to log space does not help.

Because probabilities cannot exceed 1.0, getting a very large product of probabilities -- overflow -- is not a problem. But, probabilities can be very small, and their product smaller still, so underflows (very small positive values) are a real problem, especially in contexts like Bayes nets. However, the log of very small values does not have a small absolute value, and so working in log space avoids underflow.

Working in log space does not impact the time to convergence for MLE or gradient descent.

Related Questions

---

Question : In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is a mode of the posterior distribution.
The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. Why are zero probabilities most often
a problem in maximum a posteriori estimation?

1. Zero probabilities skew the model significantly towards rare events
2. Zero probabilities causes the model to be more susceptible to overfitting
3. Access Mostly Uused Products by 50000+ Subscribers
4. Zero probabilities cause divide-by-zero errors when calculating the normalization constant


Question : Let's say, you have P(j) is the probability of seeing a given word (indexed by j) in a spam email,
this is just a ratio of counts: p(j) =n(jc) / n(c), where n(jc) denotes the number of times that word appears
in a spam email and n(c) denotes the number of times that word appears in any email. Here is the possibility
that you can get the p(j) as 0 or 1. Which of the following method can help you to reduce the chances of getting this probability as 0 or 1?


1. Naive Bayes
2. k-nearest neighbors
3. Access Mostly Uused Products by 50000+ Subscribers
4. All of the above


Question : Let's say, you have P(j) is the probability of seeing a given word (indexed by j) in a spam email, this is
just a ratio of counts: p(j) =n(jc) / n(c), where n(jc) denotes the number of times that word appears in a spam email
and n(c) denotes the number of times that word appears in any email. Here is the possibility that you can get the p(j)
as 0 or 1. Using the Laplace Smoothing method we can reduce the chances of getting this probability as 0 or 1? As below
Counts p(j) =n(jc)+A / n(c)+B

Then which of the following statement true regarding A and B


1. As long as both A > 0 and B > 0, you want very few words to be expected to never appear in spam
2. As long as both A > 0 and B > 0, you want very few words to be expected to always appear in spam
3. Access Mostly Uused Products by 50000+ Subscribers
4. All of the above.


Question : Laplacian smoothing is an algorithm to smooth a polygonal mesh. For each vertex in a mesh, a new position is chosen based on local information
(such as the position of neighbors) and the vertex is moved there. In the case that a mesh is topologically a rectangular grid (that is, each internal
vertex is connected to four neighbors) then this operation produces the Laplacian of the mesh.In Laplace smoothing, you:


1. Increase the probability mass of items seen zero times, and increase the probability mass of items seen at least once.
2. Decrease the probability mass of items seen zero times, and decrease the probability mass of items seen at least once.
3. Access Mostly Uused Products by 50000+ Subscribers
4. Increase the probability mass of items seen zero times, and decrease the probability mass of items seen at least once.




Question : Select the correct statements from the below.
1. The sum of errors will be larger than mean absolute error if errors are positive
2. The mean absolute error will, be larger than the sum if errors are negative
3. Access Mostly Uused Products by 50000+ Subscribers
4. RMSE will equal MAE if all errors are equally large
5. RMSE will be smaller if all errors are not equally large
6. RMSE will be larger if all errors are not equally large



1. 1,3,4,6
2. 1,2,4,6
3. Access Mostly Uused Products by 50000+ Subscribers
4. 2,3,5,6



Question : You are working in an ecommerce organization, where you are designing and evaluating a recommender system,
you need to select which of the following will always have the largest value?

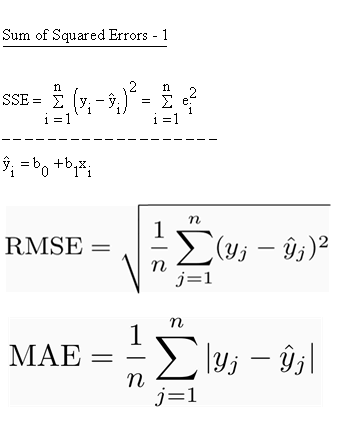
1. Root Mean Square Error
2. Sum of Squared Errors
3. Access Mostly Uused Products by 50000+ Subscribers
4. Both 1 and 2
5. Information is not good enough.